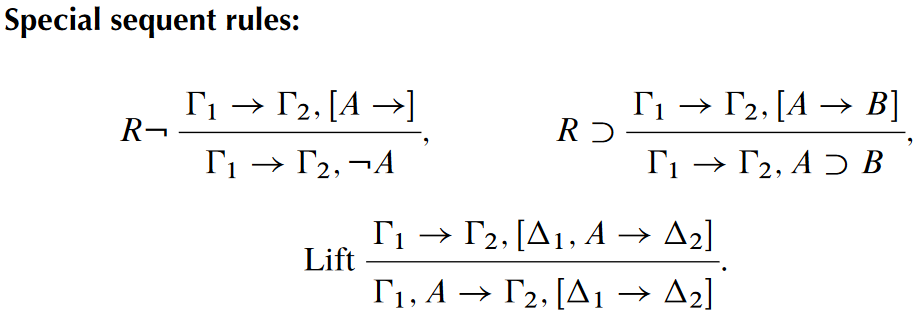(Link)

Author: Melvin Fitting (City University of New York)

Reference: M. Fitting. Nested sequents for intuitionistic logics. Notre Dame Journal of Formal Logic, 55(1):41–61, 2014. https://doi.org/10.1215/00294527-2377869

Why this paper? Cited by Syntactic Cut-Elimination for Intuitionistic Fuzzy Logic via Linear Nested Sequents and Local Intuitionistic Modal Logics and Their Calculi

About a year and a half ago I wrote about hypersequents, a modification of the tried and trusted sequent calculus approach to structural proof theory. In that setting, instead of working with a single sequent (a set of premises alongside a set of possible conclusions) we work with a list of sequents. In this paper, we look at another such modification, called nested sequents (sometimes, tree hypersequents) in which the conclusions can contain both formulae and further nested sequents. The aim is the same: by defining communication rules between different sequents, we can give structural proof theory to logics that do not have a reasonable proof theory via conventional sequents.

The concept of nested sequent has been rediscovered a few times, starting with work in the 90s by Ryo Kashima. Fitting also showed, in a slightly earlier paper, that these were essentially also a variation on an idea from the 70s called prefixed tableaux. The paper we are reading today establishes nested sequent calculus and prefixed tableaux for intuitionistic logic, including a translation from tableaux to sequents (we are told that “conversion in the other direction is also possible, but it is harder to describe and we omit it here”). Of course, intuitionistic logic has had a conventional sequent calculus since the 30s, and Fitting does not even claim priority for nested sequents for intuitionistic logic – that goes to a group from my institution, Australian National University. The goal here is to establish a clean and simple nested sequent calculus for intuitionistic logic which is amenable to extensions; modal logic is mentioned, and first-order quantifiers are investigated.

It turns out that if we add first-order quantifiers to Fitting’s calculus in a naïve way we get, not standard intuitionistic first-order logic, but rather its ‘constant domain’ version. In this logic, the domain of quantification which our ∀ and ∃ connectives are interpreted over must be the same at each possible world. This property can be expressed in a single axiom, found by Grzegorczyk in the 60s. This system for constant domain logic is the main new contribution of the paper, as previous systems for this logic lacked appealing properties. We do also see how conventional intuitionistic first-order logic can also be handled, with some modest side conditions applied to the rules of the constant domain system.