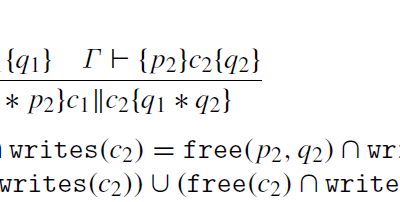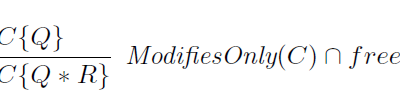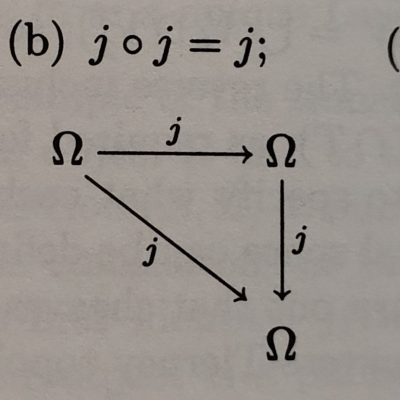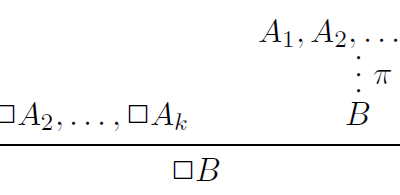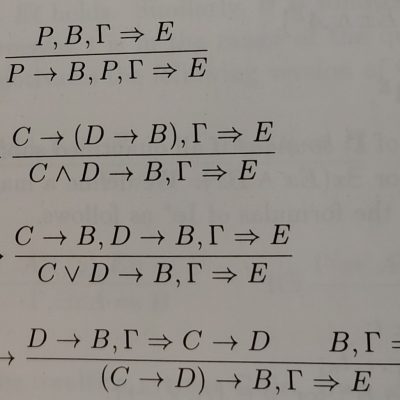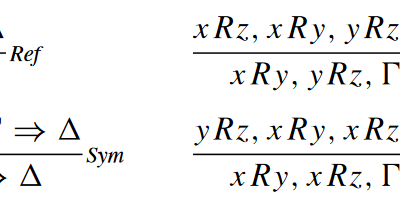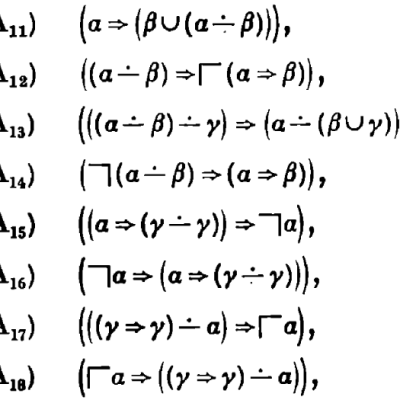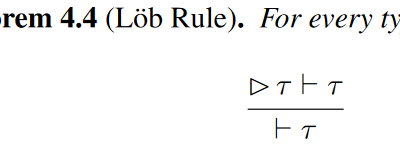-
Discussing “A semantics for concurrent separation logic”
This paper is not only cited in my recent Google Scholar recommendations (which is how I choose papers to read for my blog), but is, along with the Peter O’Hearn paper it builds on, the winner of the 2016 Gödel Prize. This prize, although nominally for any “outstanding papers in the area of theoretical computer…
-
Discussing “Z3: An Efficient SMT Solver”
The algorithm I use to supply reading for my blog (cited papers in recent articles as recommended to me by Google Scholar) sometimes sends me giant tomes, but this week I have the other extreme, at a mere four pages. This length, typical for tool demonstration papers at the conference TACAS, has not stopped this…
-
Discussing “BI as an Assertion Language for Mutable Data Structures”
I’ve written about separation logic and bunched implications for the blog before. This was the paper that brought these topics together. It constitutes a very important middle step in the early development of separation logic between Reynolds’s 2000 “Intuitionistic Reasoning about Shared Mutable Data Structures” and his 2002 “Separation Logic: A Logic for Shared Mutable…
-
Discussing “Sheaves in Geometry and Logic”
This is the second tome on topos theory I’ve read for this blog, but compared to The Elephant this one weighs in at a svelte 627 pages, and is a bit more approachable as a book to learn from, as opposed to an encyclopaedic reference. The conceit of The Elephant was that topoi can be…
-
Discussing “Extended Curry-Howard Correspondence for a Basic Constructive Modal Logic”
This is one of the classic papers – I’ve read, and cited, it a few times over the years myself – looking at extending the classic ‘Curry-Howard’ correspondence between lambda calculus and intuitionistic logic, to intuitionistic modal logic.
-
Discussing “Basic Proof Theory”
The theory of logical proofs is divided, in this well-known textbook, into two strands: structural and interpretational.
-
A Blog Update for 2025
In the semester just finished I have been snowed under revamping and teaching a big (300+ students) introductory course on Logic. If you are interested […]
-
Discussing “Proof Analysis in Modal Logic”
Modal logics of necessity and possibility do not always obviously admit an acceptable notion of structural proof theory. Yet such systems can be invaluable for both work inside the logic (proof search) and work about a logic (metatheory). This paper looks at a general framework for defining sequent calculi for a wide range of classical…
-
Discussing “An algebraic and Kripke-style approach to a certain extension of intuitionistic logic”
Heyting-Brouwer logic (more commonly known now as bi-intuitionistic logic) has fascinated me since I first learned of it. The idea is beguilingly simple: extend intuitionistic logic with a new connective that makes it completely symmetrical. The ‘symmetry’ I am thinking of (perhaps better called ‘duality’, but not quite the same thing as De Morgan duality)…
-
Discussing “A very modal model of a modern, major, general type system”
This paper is an influential landmark in the development of what is now usually called guarded recursion, following a trail that roughly goes from Nakano’s introduction of the approximation modality, to this paper, to a Dreyer, Ahmed, and Birkedal paper that I haven’t yet read for this blog but will probably eventually get to, to…
Categories
Recent Posts
- Discussing “A semantics for concurrent separation logic”
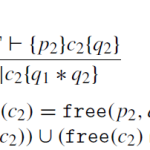
- Discussing “Z3: An Efficient SMT Solver”
- Discussing “BI as an Assertion Language for Mutable Data Structures”
- Discussing “Sheaves in Geometry and Logic”
Tags
1994 1996 2000 2001 2007 2014 2019 2021 2023 Abhishek Anand Andrew W. Appel Bedrock Systems Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Cyril Cohen Côte d'Azur University Inria Nantes INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Journal of Automated Reasoning LICS Matthieu Sozeau Metaprogramming modal logic Notre Dame Journal of Formal Logic Paul-André Melliès POPL Princeton University Proof theory Rocq Saarland University Simon Boulier Théo Winterhalter types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Valeria de Paiva