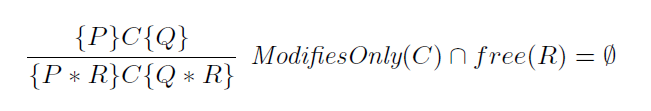(Link)

Author: Samin Ishtiaq (Queen Mary & Westfield College) and Peter W. O’Hearn (Queen Mary & Westfield College)

Reference: Ishtiaq, Samin, and Peter W. O’Hearn. “BI as an assertion language for mutable data structures.” Proceedings of the 28th ACM SIGPLAN-SIGACT symposium on Principles of programming languages. 2001.

Why this paper? Cited by Separation Logic of Generic Resources via Sheafeology and Bifurcation Logic: Separation Through Ordering

I’ve written about separation logic and bunched implications for the blog before. This was the paper that brought these topics together. It constitutes a very important middle step in the early development of separation logic between Reynolds’s 2000 “Intuitionistic Reasoning about Shared Mutable Data Structures” and his 2002 “Separation Logic: A Logic for Shared Mutable Data Structures”. Although the phrase separation logic wasn’t coined until the last of those, this paper is critical enough in the development that Ishtiaq, O’Hearn and Reynolds together can collectively be called the founders of the field.

The problem that separation logic is intended to solve is reasoning (in the Hoare logic style) about programs that directly interact with the heap (memory), particularly features like aliasing (multiple variables pointing to the same piece of memory) and dangling pointers, which are here colourfully described as “a devastatingly effective method of introducing programming errors”. Separation logic has since also been applied to other notions of resource in programming, such as permissions.

The key technology is the separating conjuncton ✱ which carries the meaning that the heap can be split into separate parts, each part satisfying one side of the conjunction. Unlike standard conjunction we usually cannot duplicate – if P holds of our heap, it is not necessarily the case that we can split the heap into two parts which each themselves satisfy P, so while we affirm ‘P and P’ we might reject P ✱ P. In this paper, unlike Reynolds’s earlier one, we also disallow weakening – we might have P ✱ Q but reject P, on the grounds that while part of the heap does satisfy P, the whole does not. This separating conjunction can be used to express for example the famous frame rule, which states that if a program takes us from a precondition P to a postcondition Q, and does not touch the memory mentioned in the logical statement R, then it also takes us from P ✱ Q to P ✱ R. In other words, we can reason modularly in terms of the memory we are directly working with, with all other conditions on the heap going harmlessly ‘along for the ride’, held apart hygienically by the separating conjunction.

The advance of this paper comes from the link to the Boolean logic of Bunched Implications (BBI), introduced a couple of years earlier by O’Hearn and Pym. In this logic separating conjunction comes equipped with a unit, which can be identified with the empty heap, and the ‘magic wand’, an implication-like connective which allows statements about all possible extensions of the current heap. Magic wand is used to establish weakest preconditions for some heap-manipulating program constructs. Setting the special separating connectives aside, the usual propositional connectives behave classically, rather than intuitionistically as in Reynolds’s precursor paper, which turns out to strictly increase the expressivity of the logic, in marked contrast to the usual situation in logic, where the classical embeds into the intuitionistic. The strictness of the expressivity improvement comes from BBI’s ability to state heap properties which are not closed under heap extension, such as “the heap as empty”. If an ‘inexact’ (extension-closed) property is desired, as if often the case if the program is not explicitly deallocating memory, it can still be expressed by announcing that the heap can be divided into two parts, one of which exactly satisfies the property of interest P, and the other of which satisfies nothing in particular – i.e. by writing P * True. Although BBI as a logic does not blend its standard and separating connectives in any interesting way (unlike the interactions of linear logic), this is a simple example of BBI as a specification language using the standard and separating parts together to useful effect.