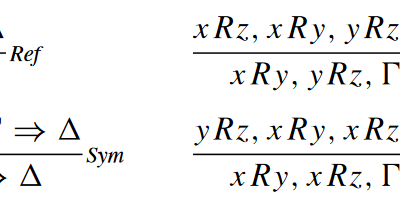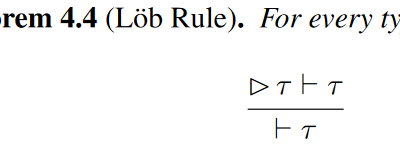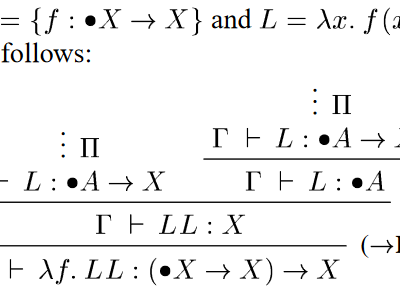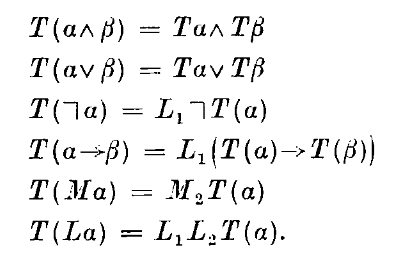Tag: modal logic
-
Discussing “Proof Analysis in Modal Logic”
Modal logics of necessity and possibility do not always obviously admit an acceptable notion of structural proof theory. Yet such systems can be invaluable for both work inside the logic (proof search) and work about a logic (metatheory). This paper looks at a general framework for defining sequent calculi for a wide range of classical…
-
Discussing “A very modal model of a modern, major, general type system”
This paper is an influential landmark in the development of what is now usually called guarded recursion, following a trail that roughly goes from Nakano’s introduction of the approximation modality, to this paper, to a Dreyer, Ahmed, and Birkedal paper that I haven’t yet read for this blog but will probably eventually get to, to…
-
Discussing “Modal Logic”
I learned modal logic from a book by Hughes and Cresswell, a pair of philosophers from my home city of Wellington, so it was interesting for me to see the very different approach taken in this week’s book, which is now the standard reference for the field ( along with the Chargrov- Zakharyaschev book of…
-
Discussing “A modality for recursion”
The algorithm I use to choose reading for this blog, pulling the most cited papers out of my Google Scholar recommendations of new papers, sometimes pops out work close to my heart; quite a few years of my own research have been direct outshoots from this paper, following its adoption by Birkedal et al., and…
-
Discussing “On modal logic with an intuitionistic base”
There is a mini-theme on this blog of important developments in intuitionistic modal logic, in which the modal notion of necessity (and, less often, possibility) is blended with the intuitionistic notion of constructive proofs which denies, for example, the law of the excluded middle. We’ve read through Plotkin and Stirling, Simpson, Davies and Pfenning, and,…
Categories
Recent Posts
- Discussing “Proof Analysis in Modal Logic”
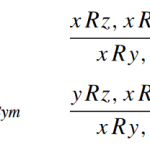
- Discussing “An algebraic and Kripke-style approach to a certain extension of intuitionistic logic”
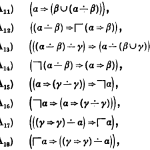
- Discussing “A very modal model of a modern, major, general type system”
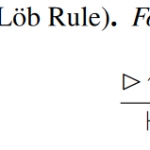
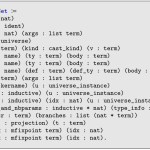
- Discussing “The MetaCoq Project”
Tags
2000 2001 2007 2014 2019 2020 2021 2023 Anupam Das Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Guarded recursion Hiroshi Nakano INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Jonathan Sterling LICS LORIA Maarten de Rijke Melvin Fitting Metaprogramming modal logic nested sequent calculus Notre Dame Journal of Formal Logic Patrick Blackburn POPL Princeton University Rocq Ryukoku University sequent calculus Sonia Marin TABLEAUX types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Université Paris 7 Yde Venema