Author: Hiroshi Nakano (Ryukoku University)
Reference: H. Nakano, “A modality for recursion,” Proceedings of the Fifteenth Annual IEEE Symposium on Logic in Computer Science (LICS), pp. 255-266, doi: 10.1109/LICS.2000.855774.
Why this paper? Cited by Deriving Dependently-Typed OOP from First Principles, Abstracting Denotational Interpreters, Intuitionistic Gödel-Löb Logic, à la Simpson, and Beyond Trees: Calculating Graph-Based Compilers
The algorithm I use to choose reading for this blog, pulling the most cited papers out of my Google Scholar recommendations of new papers, sometimes pops out work close to my heart; quite a few years of my own research have been direct outshoots from this paper, following its adoption by Birkedal et al., and I have read it several times. Re-reading an oft-used paper, like re-reading a favourite book, still has the capacity to produce surprises. This time around I realised I had forgotten how inspired Nakano was by theoretical work on object oriented programming in particular (a theme returned to by one of this week’s recommended papers).
The technical problem Nakano considers is how to understand types that are defined by self reference, in a general way that allows for those self references to appear anywhere in the definition. A common failure of such generality is the requirement that self reference cannot appear ‘negatively’ – to the left of a function arrow. For example, if Bool is the two element set, there is no set S that satisfies the equation S = S ⟶ Bool, even if we consider infinite sets and take ‘=’ as meaning ‘is isomorphic to’ – this is a classic result in set theory. Is it therefore meaningless as a type definition? This was answered in the negative in the 1980s by Macqueen, Plotkin, and Sethi, who showed how to give meaning to this via a metric. Instead of regarding our types as sets, we see them as sets that evolve over time, represented by the natural numbers, which are trivial (a singleton) at stage zero. We then take any self reference as trailing one step backwards in time. Hence S0 is trivial, S1 is S0 ⟶ Bool, which is 1 ⟶ Bool or, up to isomorphism, merely Bool, S2 is S1 ⟶ Bool, i.e. Bool ⟶ Bool, and so on. This ability to give meaning to negative self reference became part of the toolkit to express properties of object oriented programming in some work in the 90s, and more recently has turned out to be useful for program logic for some programming language features.
I should note at this point that it is not only negative self reference for which the point of view of sets as stratified over time is valuable. It is meaningful to look at a list, for example, as a data structure that reveals its first element at stage 1, its first 2 elements at stage 2, and so on, and this point of view can be used to rule out potentially bogus self referential definitions of lists where the value of the nth element of the list relies on first calculating the value of the nth or later element.
Nakano’s contribution to Macqueen et al. is to abstract away from natural number indexes by suggesting an ‘approximation modality’ ● , so that ●A holds for any A at the trivial stage zero, while at stage n+1 it holds if A held at stage n. We then require that self references be underneath (in current jargon, ‘guarded by’) the modality. So, for example, S = S ⟶ Bool remains a bad definition, but can instead be legally written as S = ●S ⟶ Bool, or perhaps = ●(S ⟶ Bool). The payoff, if self reference is suitably guarded – an easy property to check – is that every type definition you can write down is guaranteed to be meaningful. While natural number indices still exist in the semantics, they are entirely invisible in the logical syntax. It was exactly this desire for abstraction, from fiddly tracking of indices to more abstract use of a modality, that Birkedal et al. were looking for when they adapted Nakano’s modality to modify the ‘step indexing’ approach. In the modern literature Nakano’s approximation modality is usually called ‘later’ and written ▶ or ▷, and the approach is referred to as ‘guarded recursion’.
Although Nakano did “not intend to apply [his work] directly to type systems of programming language” he does present it as a (simple) type theory. The means that the underlying logic is intuitionistic, so while he notes the similarity of his modality with Gödel-Löb provability logic, no concrete relationship is suggested, because that logic is usually presented over a classical base. While soundness with respect to (realisability) semantics and termination of the type system is proved, the decidability of type checking, typability and inhabitation are left open, and indeed remain in considerable doubt given his unusual use of subtyping (avoided in most subsequent work). But while the details of the presentation can be quibbled with, as is often the case with genuinely new work, this is still a terrific paper and a real milestone in the development of connections between intuitionistic modal logic and computer science.
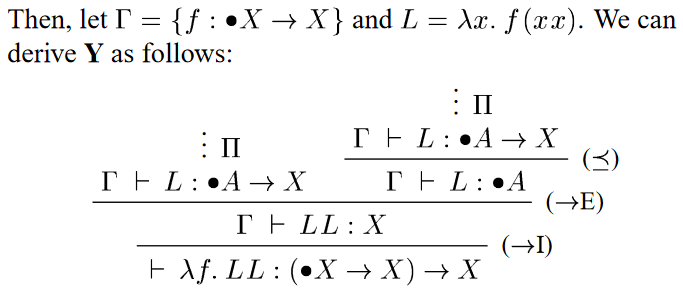
Comments
One response to “Discussing “A modality for recursion””
[…] of what is now usually called guarded recursion, following a trail that roughly goes from Nakano’s introduction of the approximation modality, to this paper, to a Dreyer, Ahmed, and Birkedal paper that I haven’t yet read for this blog but […]