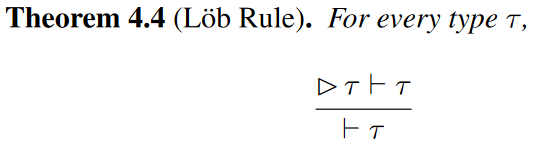(Link)

Authors: Andrew W. Appel (Princeton University / INRIA Rocquencourt), Paul-André Melliès (Université Paris 7), Christopher D. Richards (Princeton University), and Jérôme Vouillon (Université Paris 7)

Reference: Appel, Andrew W., Paul-André Mellies, Christopher D. Richards, and Jérôme Vouillon. “A very modal model of a modern, major, general type system.” In POPL ’07: Proceedings of the 34th annual ACM SIGPLAN-SIGACT symposium on Principles of Programming Languages, pp. 109-122. 2007.

Why this paper? Cited by Lewis and Brouwer meet Strong Löb and Almost-Sure Termination by Guarded Refinement

This paper is an influential landmark in the development of what is now usually called guarded recursion, following a trail that roughly goes from Nakano’s introduction of the approximation modality, to this paper, to a Dreyer, Ahmed, and Birkedal paper that I haven’t yet read for this blog but will probably eventually get to, to the ‘synthetic guarded domain theory’ paper that crystalised the field and opened the way for more advanced work on applications and type theory. The goal of all these papers was to solve problems in computer science by using a modality that allows one to express that data may be generated over time, and hence prevent unreasonable circularities (data now that depends on data I will only get later) and permit self-reference that would otherwise be impossible to model. In particular, this paper introduced the symbol ▷ and name later for the modality. Despite its influence, re-reading the paper now has revealed to me that it quite seriously diverges from both Nakano’s ideas and all work I am aware of that builds on those ideas, in a way that does not seem to have been clear to the authors at the time.

The goal of this paper is to define a type system appropriate for application to typed assembly and intermediate languages, with a slew of advanced features: intersection and union types, explicit support for addresses and mutable references, recursive types, and (impredicative) type quantification. This paper does not deal with the syntax or dynamics of such languages, instead focusing on denotational semantics. These semantics are an adaptation of Kripke frames, which I have discussed many times, e.g. here. The metaphysics of possible worlds might seem a bit abstract for application to programming languages, but the worlds of this paper are quite concrete: they are the possible contents of memory, for example defined as a partial function from locations to stored values. The modal relation then represents possible future mutations of memory, and is assumed to be irreflexive (‘later’ does not include ‘now’) and well-founded (we are only interested in what our program can do in finite time).

While Nakano would not have been surprised to see his modality used to model recursive types, the next application involving reference types is more surprising and has been influential. Here the problem is to deal with an unpleasant circularity involving worlds, whose stored values have types, and types, whose meaning is only given in the context of worlds. Without the modality, the intuitive definitions of these concepts have no solution. With the insertion of the modality, and a notion of world which includes a natural number ‘counter’, the problem can be solved.

However there is an oddity at the heart of this paper, which is that the distinctive feature of Nakano’s modality, as opposed to the famous Gödel-Löb provability modality which it resembles, is that it is defined over an intuitionistic, not classical, base. In Kripke semantics this would require that propositions true at one world must remain so at the next. Yet this is not desired for the applications of this paper, as properties of one state of memory might not hold at the next moment, as for example memory is deallocated. Without this property, we are looking at semantics for classical modal logic. Moreover, while Nakano’s modality seems to make an appearance, in fact its signature axiom (▷A → A) → A does not hold; instead we have an inference rule that if ▷A → A is a theorem then so is A. This is strictly weaker. For example A → ▷A is a consequence of Nakano’s axiom but not the inference rule, and indeed the authors specifically remark on the fact that some types do not have this property. In fact, after a discussion with my colleague Ian Shillito I believe (but have not proved) that the system of this paper is in fact plain old Gödel-Löb provability logic (whose signature axiom is ▷ (▷A → A) → ▷A). So we are left in a rather peculiar situation where the authors apparently believe they are harnessing a recent idea of Nakano, and indeed have influenced much later work that genuinely does use Nakano’s modality, but are in fact working with a logic that was codified in the 1950s!