Authors: Luis Fariñas del Cerro and Andreas Herzig (Paul Sabatier University)
Reference: del Cerro, L.F., A. Herzig, Combining classical and intuitionistic logic or: Intuitionistic implication as a conditional. In: Badder, F., and K.U. Schulz, (eds.) Frontiers of Combining Systems: FroCoS 1996, pp. 93–102. Springer, (1996)
Why this paper? Cited by Combining Intuitionistic and Classical Propositional Logic: Gentzenization and Craig Interpolation and Merging Intuitionistic and De Morgan Logics
This short but fun little paper discusses how we can combine two different logics – classical and intuitionistic – into one. Classical logic is the logic of Boole where every proposition has a definite value of True or False and negation simply inverts the value, so that ‘p or not p’ holds for any proposition p. Intuitionistic logic can be motivated in a few different ways: first, as a logic of proof, rather than truth, where negation means proved false, so that ‘p or not p’ fails for propositions not (yet) proved true or false. Second, and most relevant to this paper, in the semantics of Kripke we regard our logic as operating over a set of ‘possible worlds’, with a relation moving from one world to another as we learn new propositions, but where propositions are never forgotten on these moves. In this setting ‘not p’ is defined to hold at a world only if p fails at the world we are currently at and all possible future worlds. Again ‘p or not p’ fails, because although p might not hold at our current world, it might hold at some future world.
This paper suggests we take the standard possible worlds semantic for intuitionistic logic and add another negation, with symbol ~, to mean ‘p fails at the current world’. This works classically, as ‘p or ~p’ holds, one way or another, at every world. But it does some violence to our usual expectations of how Kripke semantics should work, because moving from world to world along our relation can now invalidate some propositions: we used to be able to assert ~p, but if we then learn p, we no longer have ~p.
The paper approaches these semantics in three different ways: via axioms, structural proof theory (semantic tableaux), and translation to the classical modal logic S4; I will focus on the axiomatics. Mindlessly combining classical and intuitionistic axioms is not sound for the intended semantics; instead, we collapse to classical logic as the two negations (and implications) become identical. The problem is isolated to the weakening axiom A ⇒ (B ⇒ A), where ⇒ is the intuitionistic implication. For example True ⇒ A means ‘in all future worlds, A holds’, but it is not valid to conclude from ~p that ‘in all future worlds, ~p holds’ (indeed this is exactly the intuitionistic negation of p!). Instead, the weakening axiom is taken to hold only where A is ‘persistent’. Syntactically this is an easy check that all classical implications and negations are in the scope of intuitionistic implications and negations (so ~p obviously fails). Semantically it enforces that if the interpretation of A holds at a world, it holds at all worlds related from it. This persistence requirement is strikingly similar to a side condition used in the program logic Iris developed decades later; I do not know how deep this analogy goes.
This paper is nearly thirty years old and has accumulated a respectable but not outstanding number of citations over that time (nearly 100 according to Google Scholar, which tends to overcount); why is it still being read and cited in 2024? Speculatively, I think the answer may have to do with one of the research directions discussed by Dov Gabbay in an interview (also with Leon van der Torre) I read recently, discovered via a Mastodon toot from José A. Alonso. If we take the point of view of logical pluralism – that there is no ‘one true logic’, but that different logics are suited to different applications – then there is a place for what Gabbay calls “logics about how to move between logics”, or more generally a formal approach to combining different logics. A similar desire to combine systems and smooth over the rough seams between them animates recent work in type theory like multimodal dependent type theory; in this setting we use modalities to travel between ‘modes’, which are different type theories that correspond to different logics. This paper, then, is a notable early contribution to this effort, although by no means the first – Prawitz’s ecumenical logic (as discussed e.g. here) and a 1979 paper by Humberstone cover quite similar ground.
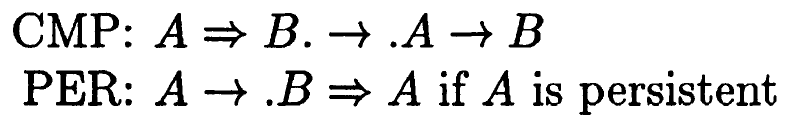
Comments
One response to “Discussing “Combining Classical and Intuitionistic Logic””
[…] semantics. These semantics are an adaptation of Kripke frames, which I have discussed many times, e.g. here. The metaphysics of possible worlds might seem a bit abstract for application to programming […]