Author: Gisèle Fischer Servi (University of Parma)
Reference: Fischer Servi, G. On modal logic with an intuitionistic base. Studia Logica 36, 141–149 (1977). https://doi.org/10.1007/BF02121259
Why this paper? Cited by Constructive S4 modal logics with the finite birelational frame property, Modal weak Kleene logics: axiomatizations and relational semantics, and Intuitionistic Gödel-Löb Logic, à la Simpson
There is a mini-theme on this blog of important developments in intuitionistic modal logic, in which the modal notion of necessity (and, less often, possibility) is blended with the intuitionistic notion of constructive proofs which denies, for example, the law of the excluded middle. We’ve read through Plotkin and Stirling, Simpson, Davies and Pfenning, and, recently, Benton, Bierman and de Paiva and will now turn our attention to one of a small string of papers Gisèle Fischer Servi wrote on this subject almost fifty years ago. Incidentally, I cannot find any information online about this pioneering logician apart from a list of papers on a University of Parma website. At the time she was publishing this work it appears to have been mostly ignored, but it is regularly cited now and I would certainly be grateful to anyone who can point me to any information about her career, even if it is in Italian.
The story of this particular paper starts with work in the 1960s by the New Zealand logician Robert Bull, who was the student of another New Zealand logician, Arthur Prior. Prior is mostly known for his invention of temporal logic (and hence is splendidly named) but essentially invented intuitionistic modal logic as well (there is apparently still earlier work by Frederic Fitch, but according to Simpson it was “rather arbitrary “ and “has not had much influence on subsequent work”). Bull took Prior’s logic MIPC and gave various arguments that it was the correct ‘intuitionistic analogue’ of the classical modal logic S5. This notion of intuitionistic analogue is more slippery that it appears, because simply adding modal axioms to an intuitionistic base instead of a classical one is not well defined, because axiomatisations are not uniquely determined, and in particular axiomatisations that define identical systems in a classical base logic do not necessarily do so in an intuitionistic one. For example, is the intuitionistic version of the ’T’ axiom □A → A, or is it ¬□A ∨ A? In classical logic, it makes no difference. In intuitionistic logic, they would define different logics!
Fischer Servi argues that Bull’s work is too specific to the details of MIPC / S5 to serve as a general framework for the notion of intuitionistic analogue of a classical modal logic, and presents a more generic construction. This construction is *verified* to map MIPC to S5 in a particular sense, and she uses this as evidence to propose that the *definition* of an intuitionistic analogue of a general model logic M should be the set of formulae that are mapped to theorems of M by the construction. This is quite an indirect way to phrase a definition, but in fact my understanding is that it holds exactly true of other later work building intuitionistic versions of modal logics by authors who were not aware of Fischer Servi’s approach, such as Plotkin and Stirling.
The details of the generic construction are quite intuitive, as an intuitionistic modal logic is mapped to a classical *bimodal* logic, where one modality corresponds to the original modality, and the other is an ‘S4’ modality capturing the intuitionistic behaviour of implication and negation. S4 is exactly the logic one would expect to be used here, because it is the logic of reflexive and transitive necessity, and reflexivity and transitivity are the core properties of intuitionistic implication (understood, for example, via Kripke frames). The core theorem, then, is that there is a syntactic translation from MIPC to classical (S4,S5)-bimodal logic that preserves and reflects theoremhood. It is hence proposed that any classical modal logic M gives rise to an intuitionistic analogue by definition, by running the translation backwards from (S4,M)-modal logic.
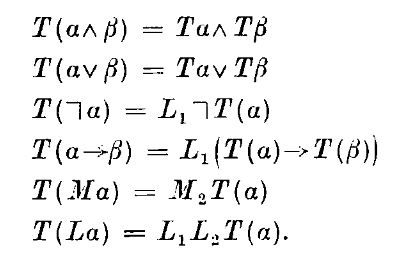
Comments
One response to “Discussing “On modal logic with an intuitionistic base””
[…] (WK) has k2 and k5; while Intuitionistic K (IK), which is the system of most interest e.g. to Fischer Servi and Simpson, has all four. CK and WK pop out naturally from proof theory, via the standard […]