Authors: Anupam Das and Sonia Marin (University of Birmingham)
Reference: Das, A., Marin, S. (2023). On Intuitionistic Diamonds (and Lack Thereof). In: Ramanayake, R., Urban, J. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2023. Lecture Notes in Computer Science, vol 14278. Springer. https://doi.org/10.1007/978-3-031-43513-3_16
Why this paper? Cited by Local Intuitionistic Modal Logics and Their Calculi , Intuitionistic Gödel-Löb Logic, à la Simpson , and Two-dimensional Kripke Semantics
I choose papers for this blog by looking at the most cited papers in my Google Scholar recommendations of recent papers. This week, my algorithm has read my mind by recommending a fairly new paper that was already at the top of my list of papers to read. Its topic, as with a few papers I’ve covered over the last few weeks, is intuitionistic modal logic, which combines the logic of constructive proof with the logic of the modalities ‘necessarily’ and ‘possibly’, usually written with a box and diamond respectively.
In fact, in a lot of the work I’ve look at, ‘possibly’ does not get a look in, with necessity-style modalities claiming full attention. The two causes of this in my view are that in a lot of applications I have looked at there is no obvious role for diamond, and because the proof theory – particularly natural deduction style proof theory, and hence type theory – for diamonds is not well understood. There may be a chicken-and-egg dynamic at work here, as lack of applications dissuades investigation into theory, and lack of good theory dissuades the developments of applications. This paper, which started life as a blog post and its fascinating comments section, reveals how deep the community’s lack of understanding of the place of intuitionistic diamond goes.
Taking some basic axioms and rules for necessity as a basis, this paper considers the following four potential axioms:
- k2: □(A ⟶ B) ⟶ ◇A ⟶ ◇B
- k3: ◇(A ∨ B) ⟶ (◇A ∨ ◇B)
- k4: (◇A ⟶ □B) ⟶ □(A ⟶ B)
- k5: ◇⊥ ⟶ ⊥
For example, read k2 as ‘if A necessarily implies B, and A is possible, then B is possible’. Various combinations of the four axioms have been considered in the literature. In particular, Constructive K (CK) has only k2; the system of Wijesekera (WK) has k2 and k5; while Intuitionistic K (IK), which is the system of most interest e.g. to Fischer Servi and Simpson, has all four. CK and WK pop out naturally from proof theory, via the standard technique for turning a classical sequent calculus into an intuitionistic one – restricting to one formula on the right (for CK) or zero or one formulae (for WK). IK pops out naturally from a different argument, namely via an intuitionistic version of the standard Gödel-Gentzen translation of modal logic to first order logic. The authors do not discuss Fischer Servi’s alternative translation to classical bimodal logic but I am fairly certain that this also yields IK.
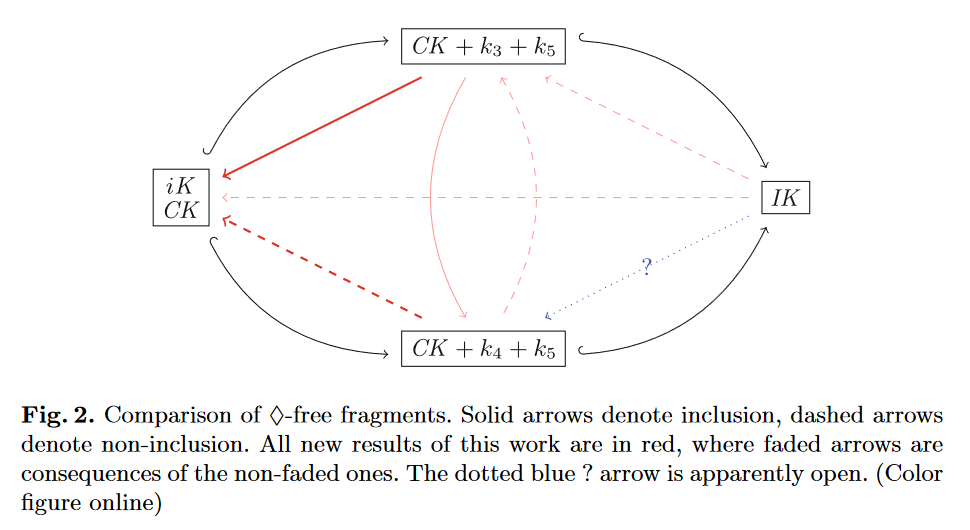
Up until now I have regarded all these systems as disagreeing only about diamond, and hence of only weak interest to the applications I’ve looked at to this date, in which diamond has no obvious role. The remarkable fact revealed by this paper is that these systems do not agree on their diamond-free fragments! In other words, even if we think we are talking only about necessity, the logic we are discussing is sensitive to which ‘complete’ modal logic is implicitly in the background. To be more precise , CK and CK + k3 + k5 (and hence WK) do agree on their ◇-free fragments, and moreover these fragments are exactly that defined by the ‘basic axioms and rules for necessity’ I glided over earlier. However, CK + k4 + k5 (and hence IK) can be distinguished from the CK family by proving, for example, ¬¬□⊥ → □⊥, which the CK family does not prove. The question of agreement between the ◇-free fragments of CK + k4 + k5 and IK remains open, so there are least two different ◇-free fragments in play – the CK and IK families – but possibly more. A further, rather remarkable, twist to the story appears in a comment by Alex Simpson to the original blog post, who recalls a PhD student in the 1990s called Carsten Grefe telling him that the ◇-free fragment of IK cannot be finitely axiomatised. Unfortunately this result, if it was indeed ever proved, was never published, and the authors of this paper have not (yet) reconstructed or falsified it.