Authors: Nick Benton (Persimmon IT Inc.), Gavin Bierman (University of Cambridge), and Valeria de Paiva (University of Birmingham)
Reference: P. N. Benton, G. M. Bierman, and V. de Paiva, “Computational types from a logical perspective,” Journal of Functional Programming, vol. 8, no. 2, pp. 177–193, 1998.
Why this paper? Cited by Ruitenburg’s Theorem mechanized and contextualized and Adjoint Natural Deduction (Extended Version)
This is a sequel to a paper by Moggi that I discussed some time ago. That paper discussed side effects, which are, roughly speaking, anything interesting that a program does other than map inputs deterministically to outputs, such as failure to terminate with a value, taking in user input, or producing output before the computation ends. Moggi noted that these effects can often be described by a particular category theoretic structure, that of a strong monad, which allows us to distinguish between ‘values of type A’ and ‘possibly effectful computations that may produce values of type A’; the latter is usually written TA. Crucially, Moggi defined a ‘computational lambda calculus’ in which T is a type former. The intention was to define a metalanguage for denotational semantics, but in fact the calculus had most impact on the practice of functional programming, with monads becoming a crucial part of the toolkit for handling effects in languages such as Haskell.
This paper regards T as a logical modality, and develops a full spectrum of proof theoretical and semantical results for Moggi’s calculus regarded as an intuitionistic modal logic. In fact the underlying logic, here called CL-logic, has been independently discovered a few times, starting with a paper by Haskell Curry in 1952; it has been also been called ‘propositional lax logic’. One thing that appears rather special about CL-logic is that it has a neat and simple natural deduction presentation, whereas many important modal logics appear to require more elaborate notions of context, as I have discussed before.
Modal logic usually makes a distinction between two different sorts of modalities: ‘necessity’ modalities which talk about truth in all possible worlds, and ‘possibility’ modalities which talk about truth in some possible world. There is some puzzlement in this paper and elsewhere about which sort of modality T is. On the one hand, we can infer TA from A – computationally, given a value in A there is a trivial computation which returns A without side effects. This is to be expected of possibility (If A is true, it is possible) but seems to trivialise the notion of necessity. On the other hand, strong monads commute with products, which in logical language means we can infer from TA and TB that T(A and B). This accords with our intuition for necessity, but seems deeply wrong for possibility: it might be possible that it will rain tomorrow and possible that it will not rain, but of course it is not possible that it will both rain and not rain. This paper plumps for T as a possibility modality and defines the possible worlds semantics in these terms, but to my eyes the definition is not very good for technical reasons (the modal relations are required to be ‘hereditary’ for all formulae without basic semantical conditions given enforcing this, so the semantics gets mixed up with the syntax). I find the definition presented by Litak, in one of my favourite papers, much more attractive, with T as a necessity modality (technically, we require that the modal relation is transitive and contains the reflexive reduction of the intuitionistic relation; see (r) and (bind) in Table 3). The perception that A implying TA trivialises the concept of necessity is simply an overhang of working with modal logics with a classical base; given an intuitionistic base, the modality remains interesting and useful.
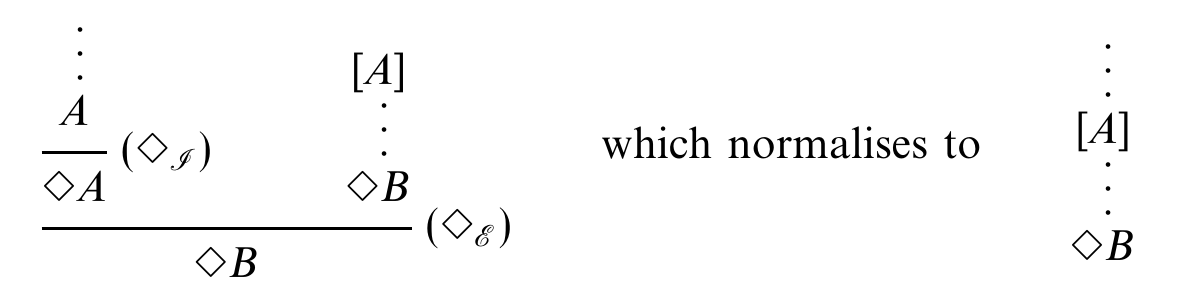
Comments
One response to “Discussing “Computational Types from a Logical Perspective””
[…] middle. We’ve read through Plotkin and Stirling, Simpson, Davies and Pfenning, and, recently, Benton, Bierman and de Paiva and will now turn our attention to one of a small string of papers Gisèle Fischer Servi wrote on […]