Author: Sara Negri (University of Helsinki)
Reference: Negri, S. Proof Analysis in Modal Logic. J Philos Logic 34, 507–544 (2005).
Why this paper? Cited by Reasoning About Group Polarization: From Semantic Games to Sequent Systems and Taking Bi-Intuitionistic Logic First-Order: A Proof-Theoretic Investigation via Polytree Sequents
Modal logics of necessity and possibility do not always obviously admit an acceptable notion of structural proof theory. Yet such systems can be invaluable for both work inside the logic (proof search) and work about a logic (metatheory). This paper looks at a general framework for defining sequent calculi for a wide range of classical modal logics. The technology for this is labelled sequent calculi, in which Kripke’s possible worlds semantics is internalised into the syntax, with assumptions and conclusions specifically labelled by which world they hold at. The relationships between worlds are then explicitly encoded in judgements, so for example wRx means that from a world w, the world x is possible.
Bringing the semantics into the syntax like this can be surprisingly controversial; I have seen the practice given the unlovely name of semantic pollution (an epithet which was apparently coined by my former Australian National University colleague and co-author Rajeev Goré!). As far as I am concerned there is a reason to prefer avoidance of labels, to allow proofs in modal logic to be ‘about’ something other than possible worlds, for example category theoretic semantics, but it does not pay to be too religious about this. If a labelled calculus for a logic of interest allows for theorems inside or about this logic to be found for which there is no obvious alternative proof method, then I have no objection.
The focus for this paper is on expanding a base calculus for classical modal logic K (for ‘Kripke’) with conditions expressing properties of the relationships between worlds. For example, the reflexivity condition, that each world is possible from itself, is expressed in the calculus by allowing us to assume wRw at any point, whereas transitivity of the relation allows to conclude wRy from wRx and xRy. The paper’s contribution is to show that any such condition expressible in first order logic in one of two, syntactically checkable, ways (as a ‘universal axiom’ or ‘geometric axiom’) can be turned into a calculus rule that obeys a number of good properties, most notably cut elimination, and these syntactic conditions are loose enough to allow for many properties of interest.
There are a number of interesting ways in which this very general work is developed within this paper. I will pick on three aspects. First, we see that one very important condition, the well-foundedness of provability (aka Gödel-Löb) logic, can be added to the system, albeit not via the generic recipe: this condition cannot be expressed in first order logic, let alone as a universal or geometric axiom. Second, the framework allows for very concise proofs that certain first order properties, expressible as universal or geometric axioms, are not expressible in modal logic: one generates the corresponding sequent calculus rule for, for example, irreflexivity, and shows that no new modal theorems follow in the supposedly stronger system. Finally, there is much discussion of decidability. Decidability often follows from structural proof theory by what is called the subformula property: roughly, for each theorem there exists a proof whose formulae are all taken from the theorem of interest. Because the theorem was only finitely long, there is therefore only a finite (albeit exponential) space of possible proofs to investigate. The subformula property immediately fails for most labelled sequent calculi: in any reflexive modal logic we can add wRw to our proof at any point, which is not part of the core language of modal logic so is not a subformula of the theorem. Instead, Negri proves a weaker version of the subformula property, and establishes decidability for a range of logics by careful arguments about upper bounds for how many such relational atoms might need to be generated while proving a given formula.
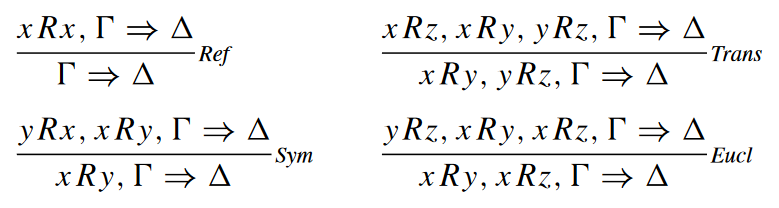
Comments
2 responses to “Discussing “Proof Analysis in Modal Logic””
I’m curious: what’s the relationship between these labeled sequent calculi and Fitch-style systems? Or do Fitch-style systems not count as “acceptably structural proof theory” for some reason?
I don’t think there is an explicit formal link in general between labelled and Fitch-style systems, but note that the systems of this paper are classical modal logics, whereas the Fitch style work that I’ve seen is used for the intuitionistic logics.