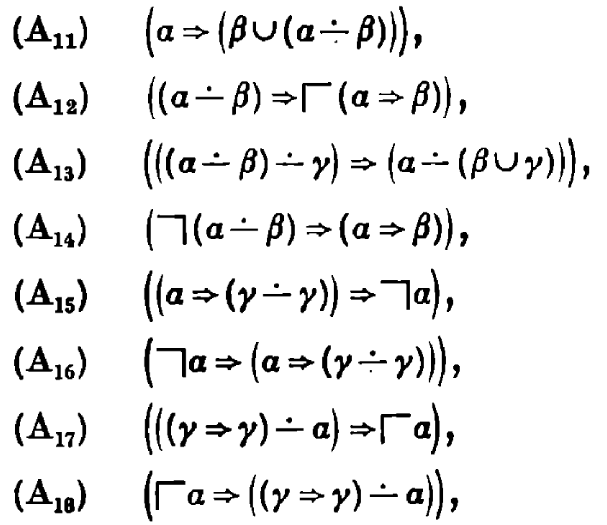(Link)

Author: Cecylia Rauszer (University of Warsaw)

Reference: Rauszer, Cecylia (1980). An algebraic and Kripke-style approach to a certain extension of intuitionistic logic. Dissertations Mathematicae, Polish Scientific Publishers, pp. 1–67.

Why this paper? Cited by Rules of Explosion and Excluded Middle: Constructing a Unified Single-Succedent Gentzen-Style Framework for Classical, Paradefinite, Paraconsistent, and Paracomplete Logics and Taking Bi-Intuitionistic Logic First-Order: A Proof-Theoretic Investigation via Polytree Sequents

Heyting-Brouwer logic (more commonly known now as bi-intuitionistic logic) has fascinated me since I first learned of it. The idea is beguilingly simple: extend intuitionistic logic with a new connective that makes it completely symmetrical. The ‘symmetry’ I am thinking of (perhaps better called ‘duality’, but not quite the same thing as De Morgan duality) is already exhibited by most of the propositional connectives: truth, which is entailed by everything, is dual to falsity, which entails everything; conjunction, which is a sort of greatest lower bound, is dual to disjunction, which is a least upper bound. But implication (and hence negation, which is definable via implication and false) has no dual in this way. What happens if we ‘fix’ this?

We get a new binary connective which Rauszer writes ‘∸’ and calls ‘Brouwerian implication’ and ‘pseudo-difference’. It has gone by various symbols and names over the years including ‘subtraction’, ‘coimplication’, and ‘exclusion’; I have taken to pronouncing p ∸ q as ‘p without q’ because that is the best fit in natural language I can make with my intuition (warning: this is purely my invention and does not appear in the literature!). It is not hard to define via symmetry: just as implication can be defined  by ‘residuation’ with conjunction, ‘p and q entails r’ exactly if ‘p entails q implies r’, we use disjunction: ‘p ∸ q entails r’ exactly if ‘p entails q or r’. Now just as we can define negation from implication, with ‘not p’ and ‘p implies false’, we can define another notion of negation on p as ‘true ∸ p’.

It’s worth taking a moment to enjoy some of the odd properties of this logic. First, the usual negation of p implies the dual negation of p, but not vice versa; for this reason, the dual negation is now often called ‘weak negation’. Weak indeed, because weak negation is not ‘explosive’: there is no contradiction in general between p and weak-not p. Weak negation instead satisfies the law of the excluded middle! Have we collapsed to classical logic, then? One of the contributions of this paper (already known from earlier work by Rauszer I believe, but with a particularly pleasant proof here) is that bi-intuitionistic logic is in fact conservative over intuitionistic logic, so any theorem of this logic that does not use ∸ holds exactly if it holds in intuitionistic logic. Therefore while bi-intuitionistic logic is clearly not a constructive logic – its weak law of the excluded middle contradicts the disjunction property – is it has constructive logic nicely contained inside it. If we do collapse to classical logic then ‘p ∸ q’ collapses to ‘p and not q’ (just as ‘p implies q’ collapses to ‘not p or q’).

So much for the syntactic view – what does this new connective mean? This paper gives answers in both algebraic and Kripke style; I will focus on the Kripke frames approach. In fact bi-intuitionistic logic can be interpreted in the exact same models as the usual intuitionistic logic (making the conservativity result obvious). We have a set of ‘possible worlds’ with a reflexive and transitive relation between them, and all propositions are preserved by this relation. We think of the relation as moving from one state of knowledge to another, learning new facts but never forgetting old ones. In this setting ‘p implies q’ asks that for all future worlds, either p fails, or q holds. By duality p ∸ q means that there exists a past world where p holds and q fails. Similarly, the usual negation of p asks that p fails in all future worlds, whereas the weak negation of p says that p fails in some past world. We can now see why the weak negation is not explosive (it could be that p failed in the past, but now holds), and satisfies excluded middle (if p does not currently hold, it fails at a past world – by reflexivity, the current world will do as a witness). This also gives a different view of how the logic is not constructive; p ∸ q holds if we can construct p in a way that does not require q be constructible, but the latter notion is not itself a construction.