(Link)

Author: Jonathan Sterling (Carnegie Mellon University)

Reference: Sterling, J. (2021). First Steps in Synthetic Tait Computability: The Objective Metatheory of Cubical Type Theory [PhD thesis, Carnegie Mellon University],

Why this paper? Cited by Layered Modal Type Theory: Where Meta-programming Meets Intensional Analysis, Primitive Recursive Dependent Type Theory, and Parametricity via Cohesion

I’ve been meaning to get more familiar with this dissertation for a while (reading it thoroughly would take longer than the week I try to take for my blog posts), after its ideas were used in a paper I discussed last year. This thesis presents a new technique, synthetic Tait computability, for proving the ‘syntactic’ properties of canonicity and normalisation in type systems, with the previously unproven normalisation result for cubical type theory as its highlight.

Type theories, such as the on-paper type theories of Martin-Löf or implementations such as Coq/Rocq and Lean, require that all programs terminate. It is otherwise possible to ‘prove’ falsehoods (any contradiction, considered as a type, can be inhabited by a program that does not terminate and so never has to deliver its impossible result). Furthermore, when one has dependent types, type checking might need to run arbitrary code, so general termination is essential to have decidable type checking. Reading ‘type checking’ as ‘proof checking’, this accords with our intuition that while developing a proof may be very difficult or impossible, checking its correctness should be possible in finite time by anyone suitably qualified – if it is not, it hardly qualifies as a proof! Termination, also called normalisation, is not enough however; a language which cannot be run at all is obviously terminating, but not of much use. The property of canonicity asks that (at least at certain observable types) all programs with no free variables compute to some sensible notion of value, not getting ‘stuck’ prematurely. This is the essence of constructive mathematics, where a proof that, for example, there exists a number with a certain property must provide one such number as evidence. That number need not be obviously visible in the proof, but the proof, if run as a program, should be able to compute it explicitly.

How do we prove that our type system of choice has these desirable properties? There are many techniques, the one best known to me being Tait’s method as presented by Girard in his wonderful Proofs and Types. Unfortunately these techniques can feel rather ad hoc and fragile, often needing to be reconstructed from scratch in response to mild extensions of the type theory or alterations of the syntax. In his thesis Sterling (in part, with collaborators) introduces a new bag of tricks based on category theory which aim to add regularity and rigour to this process.

Following his section 4.2, it might be worthwhile to start by looking at how this all plays out in the somewhat familiar setting of the canonicity of the simply typed lambda calculus. The first thing to note is that Sterling does not prove anything in particular about the standard presentation of this calculus in terms of various textual symbols, Curry vs Church typing for variables, explicit rules for beta-reduction etc. Instead the syntax is defined in what he terms the ‘objective’, or ‘presentation-invariant’ style, as the free Cartesian closed category on a simple base type. In part this means that all the equations of the theory are built in and do not exist separately from the raw syntax. This is extremely well motivated in the case of the simply typed lambda calculus, whose relationship to Cartesian closed categories is long established. However I do find Sterling’s fierce rhetoric regarding work with concrete syntax (“regrettable”, “ill-advised”, “junk-theorems”, etc.) to in general be over the top; when we move to less familiar notions we would like to develop usable type theory for, a bridge will always need to be built to concrete syntax, and I doubt this will always be easy.

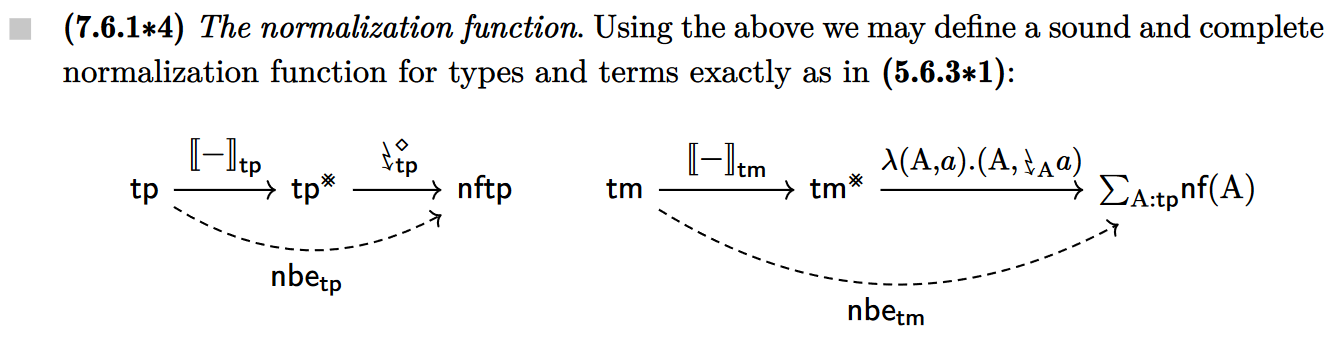
Having established our setting, which organises into a category of judgements, we then pick out the judgements we are interested in by means of a functor called a ‘figure shape’. In the case of canonicity for the simply type lambda-calculus we care about the closed judgements, in which case our figure shape corresponds to the ‘global elements’ of our category of judgements, picking out exactly the judgements with empty context. The figure shape gives rise to an ‘Artin gluing’ category of ‘computability structures’. The proof of canonicity can then be given if we can define a suitable functor from judgements to the Artin gluing category, whose construction may require some ingenuity. The details of defining this functor for simple types strongly resemble those of standard techniques of Tait, motivating the name of this approach. Done successfully, a very simple diagram chase involving our functor concludes that all elements of our base type are equal to one of the values of the base type, as required. The proofs of normalisation, and for Martin-Löf and cubical type theory, have essentially the same shape, although the details require much more work and ingenuity. Much bureaucratic work in the definition of the required functor can be avoided by embedding our Artin gluing category into a ‘normalisation topos’ within which we can work synthetically, but this step has not been fully absorbed by me in the confines of this week; the use of modal logic in this section looks very interesting, however.

One last thing to note is that the normalisation functor developed during the proof is not necessarily computable. A separate, but in the case of the systems of this thesis, very simple, argument is necessary to show that this is so. I think it is fair to say that this argument gets very little clue of how normalisation actually could or should be implemented in practical style on real syntax, but it is no small matter to show that it is indeed possible, particularly in the case of cubical type theory.