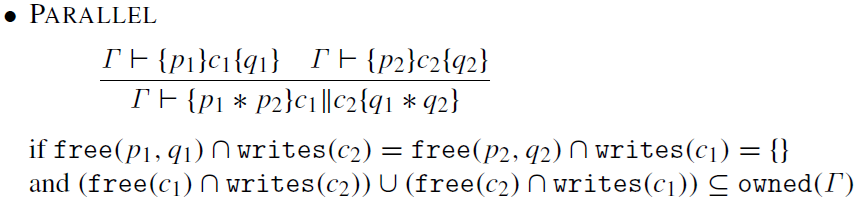(Link)

Author: Stephen Brookes (Carnegie Mellon University)

Reference: Stephen Brookes, A semantics for concurrent separation logic, Theoretical Computer Science, Volume 375, Issues 1–3, 2007, Pages 227-270

Why this paper? Cited by Shaking up the foundations of modern separation logic, Beyond Concurrent Separation Logic: Who is Afraid of Completeness Proofs?, and Compositional Verification in Concurrent Separation Logic with Permissions Regions

This paper is not only cited in my recent Google Scholar recommendations (which is how I choose papers to read for my blog), but is, along with the Peter O’Hearn paper it builds on, the winner of the 2016 Gödel Prize. This prize, although nominally for any “outstanding papers in the area of theoretical computer science” almost always goes to ‘Theory A’ (Algorithms, automata, complexity and games) rather than ‘Theory B’ (Logic, semantics and theory of programming’), making this classic paper an interesting outlier.

Separation logic has been a common topic for this blog to return to, for example here and here. Although its applications have grown over time, the fundamental motivation has been programming with pointers. Multiple pointers directed to the same part of the memory heap, and deallocated pointers that point nowhere, are tricky sources of program bugs and hard to reason about with older logical techniques. Separation logic allows one to talk not merely about which propositions hold in a particular state, but to express that certain propositions hold ‘separately’, in the sense of relying on disjoint parts of memory. In particular, a ‘frame rule’ allows one to reason modularly about fragments of a program, under the assumption that no other part of the program can interfere with that part’s memory resources.

This paper concerns the combination of pointer programming with concurrency, another rich source of errors, confusion, and logical difficulty. In particular, the desire is to avoid races, “in which one process changes a piece of state that is simultaneously being used by another process” (deadlocks, where parallel processes prevent each other from proceeding, are only briefly discussed in a paper mostly concerned with partial, rather total, correctness). The O’Hearn paper mentioned above made some suggestions for separation logic rules to tame this problem, while this paper introduces a semantics that allow such rules to be validated.

These semantics are defined in terms of sets of traces, sequences of actions that interact with memory. Parallel compositions are two programs then ranges across all possible interleavings of the actions from each programs’ traces. Races, in which the free identifier of one action intersect with the write action of an action that is supposed to run in parallel, are treated as always a catastrophic failure, so that any proof that goes through is, by soundness, guaranteed to be race free. The key and non-obvious technical insight that makes it all work is to restrict certain invariants to be precise: if it satisfied by a heap, it cannot be satisfied by any extension of that heap.