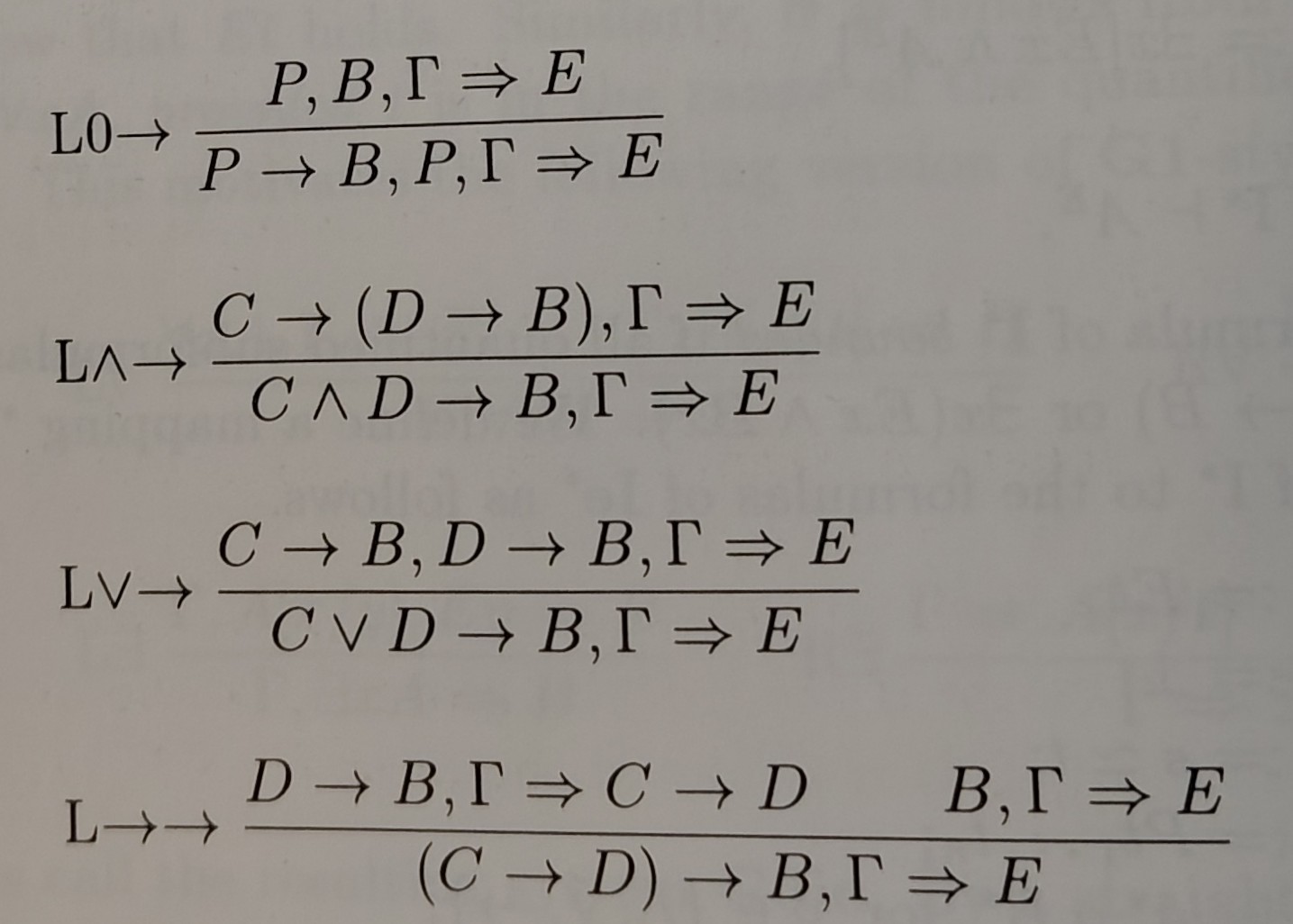(Link)

Author: A. S. Troelstra (University of Amsterdam) and Helmut Scwichtenberg (University of Munich)

Reference: The most recent edition is: Troelstra, A. S., and H. Schwichtenberg. Basic proof theory, 2nd edition. Cambridge Tracts in Theoretical Computer Science No. 43. Cambridge University Press, 2000. But I was more easily able to get hold of the 1996 1st edition.

Why this paper? Cited by Proof Search and Countermodel Construction for iCK4, Intuitionistic monotone modal logic via translation, Bounded Inquisitive Logics: Sequent Calculi and Schematic Validity, and Gödel’s modal interpretation of intuitionistic logic and its proof theory.

The theory of logical proofs is divided, in this well-known textbook, into two strands: structural and interpretational.

Structural proof theory was the subject of another textbook I wrote about not too long ago on this blog, so to avoid repeating myself I will only briefly recap that it is the art, craft, and science of proof systems that require proofs be organised in some rigid way. One could contrast this to ‘ordinary mathematics’, which is very interested in proofs but imposes no particular formal conditions on how they are presented or structured, so long as each step is an acceptable mathematical manoeuvre and, perhaps, the whole is sufficiently ‘elegant’. The ability to express all proofs of interest within a particular structure can allow metaproofs about certain logics, such as of their consistency, because logicians can meaningfully make statements about the space of all possible proofs. Further, in developments that began well before the release of this book but began to bear serious fruit a bit later than that, these ideas have provided the foundations for machine-checkable mathematics, because the rigid syntax, and support for algorithmic generation and manipulation of proofs, of structural proof theory is just what is required for machine mathematics.

Interpretational proof theory, which is a more minor theme of this work, is about how the syntax of one logic can be transformed into the syntax of another in a way that preserves validity. This allows one logic to interpret another, and helps establish the relative strengths of different logics. For example, intuitionistic logic (the logic of constructive proof) appears at first to be a sublogic of classical logic, as it can be directly defined by deleting a certain axiom from classical logic, but in fact there exists an interpretation of classical logic in intuitionistic logic. This translation, originally by Kolmogorov and turning 100 this year, confounds our expectations by showing that intuitionistic logic is in some sense stronger than classical logic – so long as we translate, we can use intuitionistic logic to answer questions about the validity of classical logic arguments, but classical logic cannot do the same job for intuitionistic logic.

This book is probably not suitable for an introduction to logic, although I am always reluctant to say things like that outright, on the grounds that there might be some student out there whom it suits perfectly. But for a person with some background in logic who is getting interested in proofs (as opposed to, say, models), it is an excellent resource, if perhaps more of a reference book than a teaching book. I personally knew of most of the material in broad outline, but there were many details on which this book could refresh me, and the good historical notes ending each chapter have sent me down an interesting little rabbit hole to investigate some 1970s work by Dag Prawitz, which is just the sort of thing I hope for when I read things for this blog.