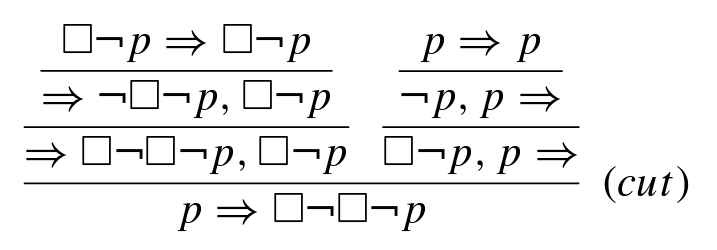(Link)

Author: Hiroakira Ono (Japan Advanced Institute of Science and Technology)

Reference: Ono, Hiroakira. Proof Theory and Algebra in Logic. Springer, 2019.

Why this paper? Cited by Combining Intuitionistic and Classical Propositional Logic: Gentzenization and Craig Interpolation and Generating proof systems for three-valued propositional logics

I was pleased to see this book bubbling up through my recommendations, as I once saw a keynote talk by Hiroakira Ono at a logic conference in my former home city of Wellington and it was one of the most cogent and exciting logic talks I’ve ever enjoyed. Ono’s textbook is split into two parts, which can for the most part be read separately: one on sequent calculus and one on abstract algebra for logic.

The first section concerns structural proof theory, a topic I have written about for this blog before. Unlike Negri and von Plato’s book, Ono focuses only on propositional logic without quantifiers, and on sequent calculus. The sequent calculus is a system where one works on lists of premises and conclusions (or for some logics, only a single conclusion) and can apply ‘left’ and ‘right’ rules to manipulate either list. Sequent calculi may be less ‘natural’ than the structural proof theory appropriately named natural deduction, but are an ideal tool for proving theorems about a logic. The key result here is cut elimination, where one shows that any proof that is structured around an intermediate lemma can be transformed into a proof in which that lemma is cut out and only the primitive, highly structured, left and right rules are used. This result is not merely interesting in its own right, but is the crucial lemma towards a whole bunch of results like decidability, the subformula property, Craig’s celebrated interpolation property, and a number of others. Ono casts his net widely into classical, intuitionistic, modal, substructural, and intermediate logics to observe how these theorems change, or fail, given different combinations of proof rules. For example the rather austere FL_c, a ‘Full Lambek’ substructural logic where formulae can be contracted but not weakened or even exchanged, fails to be decidable even though most ‘nearby’ logics do enjoy this property.

The second section looks at algebraic approaches to logic. This would be familiar to many through Boolean algebras and perhaps their intuitionistic cousins, the Heyting algebras, but again Ono looks wider than these to apply his techniques to a whole variety of logics, including fuzzy logics. This stuff gets really exciting for me when the ‘detour’ through algebra results in powerful results about logics which have not been achieved through other means. The highlight of this for me (stated but not proved in this book) is the remarkable result of Larisa Maksimova showing through an algebraic argument that exactly and only seven of the uncountably many logics that lie between intuitionistic and classical logic have Craig’s interpolation property.

To make a negative comment to end this discussion, the number of typos in the prose in this book is quite high; it does not even seem to have been spell checked. I hope that the technical material is not similarly sloppy but I did not read it enough detail this week to be sure.