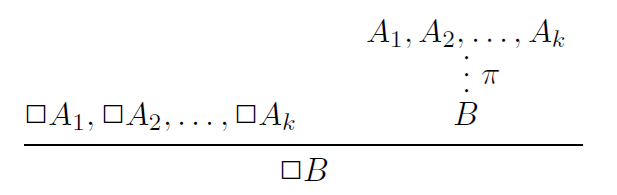(Link)

Author: Gianluigi Bellin (University of Verona), Valeria de Paiva (Xerox Palo Alto Research Center), and Eike Ritter (University of Birmingham)

Reference: Gianluigi Bellin, Valeria de Paiva, and Eike Ritter. Extended Curry-Howard correspondence for a basic constructive modal logic, in Proceedings of Methods for Modalities (M4M) (2001)

Why this paper? Cited by Paraconsistent Constructive Modal Logic, Intuitionistic monotone modal logic via translation, Higher-order Kripke models for intuitionistic and non-classical modal logics, and Justification Logic for Intuitionistic Modal Logic (Extended Technical Report)

This is one of the classic papers – I’ve read, and cited, it a few times over the years myself – looking at extending the classic ‘Curry-Howard’ correspondence between lambda calculus and intuitionistic logic, to intuitionistic modal logic. It in particular looks at the logic CK (for Constructive Kripke), a very minimal notion of intuitionistic modal logic; it is the weakest logic I discussed in this post, for example. However, unlike much of the literature in this area, this paper does not neglect the diamond, or possibility, operator, but considers it alongside the usual box, or necessity, operator. Further, the word ‘extended’ in the title refers to a connection with category theory, which was a novelty for work in this area at the time.

How do we design a lambda calculus whose inhabited types correspond to the theorems of (some notion of) intuitionistic modal logic? It has been found convenient by many to change the definition of a context to express more structure between the variables. This idea involves either a ‘dual context’ and ‘Fitch-style’ approach, as I discussed on this blog some time ago. Both of these approaches continue to be worked with today, including in calculi with advanced features such as dependent types and univalence; see for example my post on a paper that applies dual context type theory to a problem with cubical type theory, or the Fitch-style development of Multimodal Dependent Type Theory. This week’s paper discussed both these approaches, but notes that neither have been connected to category theory, and in neither case has diamond been integrated. The former weakness has been corrected in the intervening years (for dual contexts, by Kavvos; for Fitch-style, by me), but the latter remains a problem. One advance this paper does make in this area is to sketch a dual context system for CK (without diamond) whereas prior work with dual contexts involved (a constructive version of) the stronger modal logic S4.

The main thrust of the paper, however, is to show that a modal lambda calculus can be defined for CK without resort to exotic structure on the context at all. This involves a simultaneous substitution over all variables in a context, so the calculus could still be regarded as unusual: the novel proof rules can have an unbounded number of premises, because a judgement could have any number of variables, and each of them needs to dealt with individually. I was once part of a research effort that looked at certain applications of this simultaneous substitution approach, but when we turned to dependent types we found carrying these sometimes massive substitutions around in our types and terms too unwieldy to tolerate – note that this was an aesthetic or quality of life judgement, not any formal problem with the approach of this paper! Since then I am not aware of anyone else attempting to use simultaneous substitutions of this sort in dependent type theory, but this paper remains a milestone in the space of possible developments of modal calculi, and an inspiration in particular to those who care about the modal diamond.