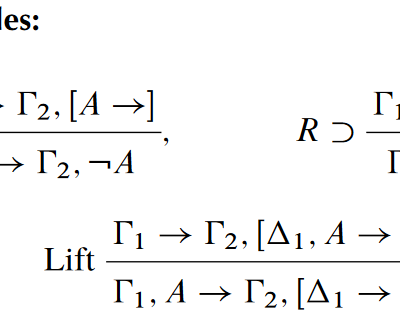Tag: 2014
-
Discussing “Nested Sequents for Intuitionistic Logics”
About a year and a half ago I wrote about hypersequents, a modification of the tried and trusted sequent calculus approach to structural proof theory. In that setting, instead of working with a single sequent (a set of premises alongside a set of possible conclusions) we work with a list of sequents. In this paper,…
Categories
Recent Posts
- Discussing “A semantics for concurrent separation logic”
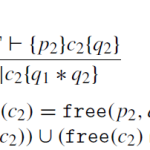
- Discussing “Z3: An Efficient SMT Solver”

- Discussing “BI as an Assertion Language for Mutable Data Structures”
- Discussing “Sheaves in Geometry and Logic”
Tags
1994 1996 2000 2001 2007 2014 2019 2021 2023 Abhishek Anand Andrew W. Appel Bedrock Systems Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Cyril Cohen Côte d'Azur University Inria Nantes INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Journal of Automated Reasoning LICS Matthieu Sozeau Metaprogramming modal logic Notre Dame Journal of Formal Logic Paul-André Melliès POPL Princeton University Proof theory Rocq Saarland University Simon Boulier Théo Winterhalter types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Valeria de Paiva