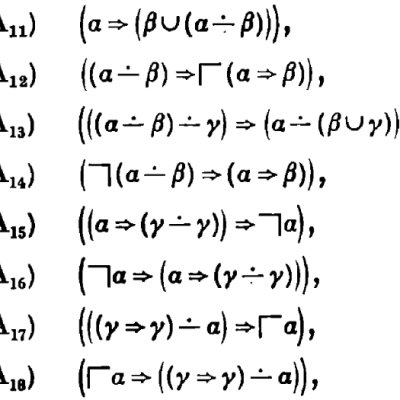Tag: Bi-intuitionistic logic
-
Discussing “An algebraic and Kripke-style approach to a certain extension of intuitionistic logic”
Heyting-Brouwer logic (more commonly known now as bi-intuitionistic logic) has fascinated me since I first learned of it. The idea is beguilingly simple: extend intuitionistic logic with a new connective that makes it completely symmetrical. The ‘symmetry’ I am thinking of (perhaps better called ‘duality’, but not quite the same thing as De Morgan duality)…
Categories
Recent Posts
- Discussing “Proof Analysis in Modal Logic”
- Discussing “An algebraic and Kripke-style approach to a certain extension of intuitionistic logic”
- Discussing “A very modal model of a modern, major, general type system”
- Discussing “The MetaCoq Project”
Tags
2000 2001 2007 2014 2019 2020 2021 2023 Anupam Das Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Guarded recursion Hiroshi Nakano INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Jonathan Sterling LICS LORIA Maarten de Rijke Melvin Fitting Metaprogramming modal logic nested sequent calculus Notre Dame Journal of Formal Logic Patrick Blackburn POPL Princeton University Rocq Ryukoku University sequent calculus Sonia Marin TABLEAUX types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Université Paris 7 Yde Venema