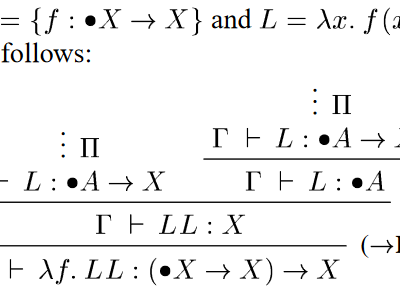Tag: LICS
-
Discussing “A modality for recursion”
The algorithm I use to choose reading for this blog, pulling the most cited papers out of my Google Scholar recommendations of new papers, sometimes pops out work close to my heart; quite a few years of my own research have been direct outshoots from this paper, following its adoption by Birkedal et al., and…
-
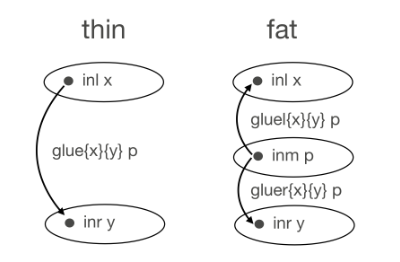
Discussing “A Mechanization of the Blakers–Massey Connectivity Theorem in Homotopy Type Theory”
I first became aware of this paper from a long and fascinating blog comment thread in which mathematicians argued about the utility, or lack thereof, of homotopy type theory for homotopy theorists. Urs Schreiber, arguing for team HoTT, held up this paper an exemplar of the value of the type theoretical approach, saying “it was…
Categories
Recent Posts
- Discussing “A semantics for concurrent separation logic”
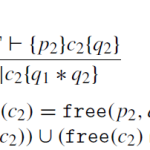
- Discussing “Z3: An Efficient SMT Solver”

- Discussing “BI as an Assertion Language for Mutable Data Structures”
- Discussing “Sheaves in Geometry and Logic”
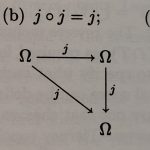
Tags
1994 1996 2000 2001 2007 2014 2019 2021 2023 Abhishek Anand Andrew W. Appel Bedrock Systems Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Cyril Cohen Côte d'Azur University Inria Nantes INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Journal of Automated Reasoning LICS Matthieu Sozeau Metaprogramming modal logic Notre Dame Journal of Formal Logic Paul-André Melliès POPL Princeton University Proof theory Rocq Saarland University Simon Boulier Théo Winterhalter types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Valeria de Paiva