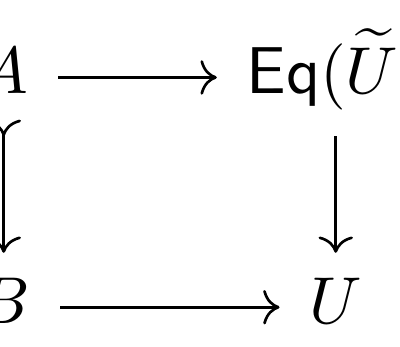Tag: University of San Diego
-
Discussing “All (∞,1)-Toposes Have Strict Univalent Universes”
I have written before about 2-category theory, where we have objects, arrows between objects, and arrows (sometimes called 2-cells) between those arrows. The canonical example are collections of categories, which have layers of categories; functors; and natural transformations. ∞-categories generalise this to an infinite stack of layers of n-cells. An (∞,1)-category is a special case…
Categories
Recent Posts
- Discussing “Proof Analysis in Modal Logic”
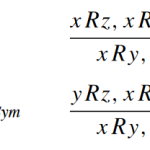
- Discussing “An algebraic and Kripke-style approach to a certain extension of intuitionistic logic”
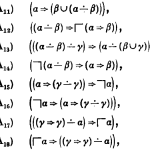
- Discussing “A very modal model of a modern, major, general type system”
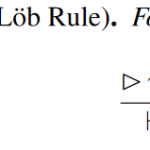
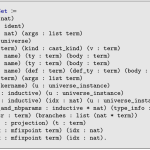
- Discussing “The MetaCoq Project”
Tags
2000 2001 2007 2014 2019 2020 2021 2023 Anupam Das Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Guarded recursion Hiroshi Nakano INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Jonathan Sterling LICS LORIA Maarten de Rijke Melvin Fitting Metaprogramming modal logic nested sequent calculus Notre Dame Journal of Formal Logic Patrick Blackburn POPL Princeton University Rocq Ryukoku University sequent calculus Sonia Marin TABLEAUX types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Université Paris 7 Yde Venema