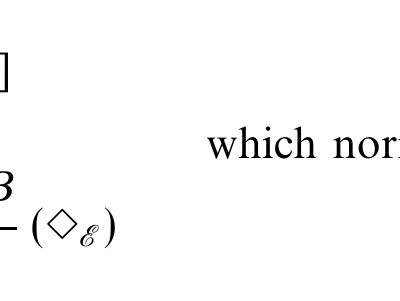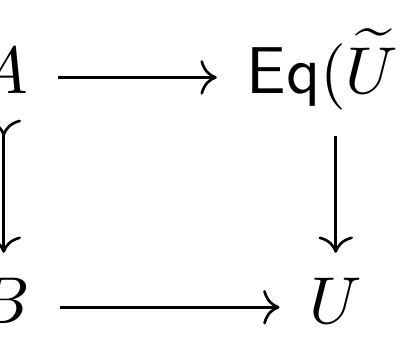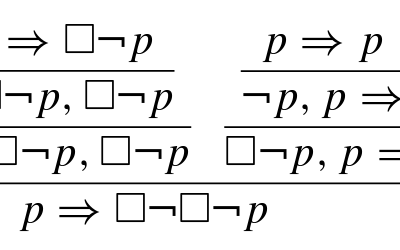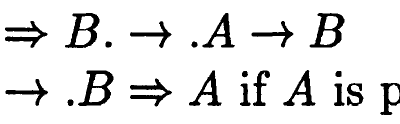-
Discussing “All (∞,1)-Toposes Have Strict Univalent Universes”
I have written before about 2-category theory, where we have objects, arrows between objects, and arrows (sometimes called 2-cells) between those arrows. The canonical example are collections of categories, which have layers of categories; functors; and natural transformations. ∞-categories generalise this to an infinite stack of layers of n-cells. An (∞,1)-category is a special case…
-
Discussing “Proof Theory and Algebra in Logic”
I was pleased to see this book bubbling up through my recommendations, as I once saw a keynote talk by Hiroakira Ono at a logic conference in my former home city of Wellington and it was one of the most cogent and exciting logic talks I’ve ever enjoyed. Ono’s textbook is split into two parts,…
-
Discussing “Isabelle/HOL: A Proof Assistant for Higher-Order Logic”
In the world of interactive theorem provers two systems stand out for their maturity and wide adoption. One is Rocq, until recently known as Coq, about which I have written previously; Isabelle/HOL, the topic of this week’s reading, is the other. Rocq is one of a number of systems (for example, Lean) based on Martin-Löf’s…
-
Discussing “Combining Classical and Intuitionistic Logic”
This short but fun little paper discusses how we can combine two different logics – classical and intuitionistic – into one. Classical logic is the logic of Boole where every proposition has a definite value of True or False and negation simply inverts the value, so that ‘p or not p’ holds for any proposition…
-
Discussing “Domain Theory”
Domains are certain forms of ordered sets used to address problems in the denotational semantics (mathematical interpretation) of programming languages. The area was invented by Dana Scott in a series of papers starting in 1969, building on earlier work by many others that used lattices. This book (which admittedly, I did not have time to…
-
Welcome to The Updated Scholar!
Welcome to the new version of my blog The Updated Scholar, previously hosted by blogspot. This blog exists mostly for me, and perhaps also as […]
Categories
Recent Posts
- Discussing “Z3: An Efficient SMT Solver”
- Discussing “BI as an Assertion Language for Mutable Data Structures”
- Discussing “Sheaves in Geometry and Logic”
- Discussing “Extended Curry-Howard Correspondence for a Basic Constructive Modal Logic”
Tags
1994 1996 2000 2001 2014 2019 2020 2021 2023 Andrew W. Appel Bedrock Systems Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Côte d'Azur University Fabian Kunze Gregory Malecha Inria Nantes intuitionistic logic intuitionistic modal logic Jonathan Sterling Journal of Automated Reasoning LICS Matthieu Sozeau Metaprogramming modal logic Nicolas Tabareau Notre Dame Journal of Formal Logic Paul-André Melliès POPL Princeton University Proof theory Rocq Saarland University Théo Winterhalter types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Valeria de Paiva