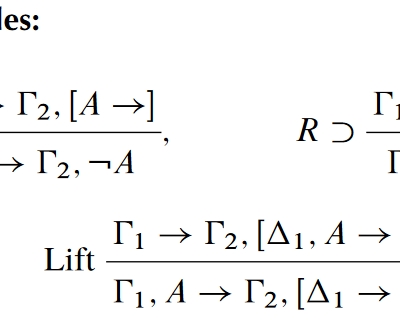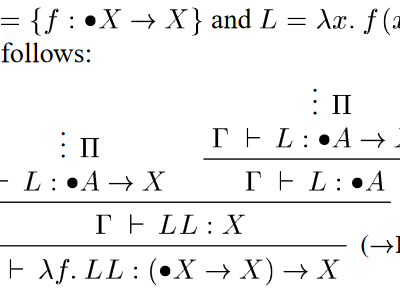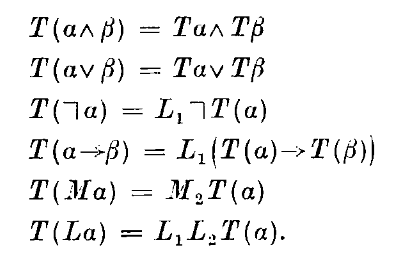-
Discussing “First Steps in Synthetic Tait Computability: The Objective Metatheory of Cubical Type Theory”
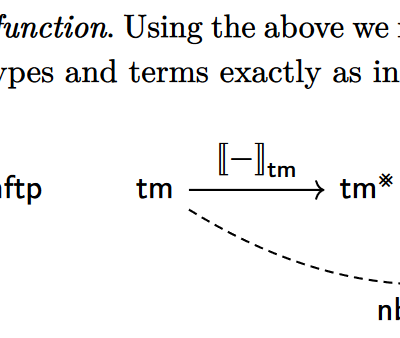
I’ve been meaning to get more familiar with this dissertation for a while (reading it thoroughly would take longer than the week I try to take for my blog posts), after its ideas were used in a paper I discussed last year. This thesis presents a new technique, synthetic Tait computability, for proving the ‘syntactic’…
-
Discussing “Nested Sequents for Intuitionistic Logics”
About a year and a half ago I wrote about hypersequents, a modification of the tried and trusted sequent calculus approach to structural proof theory. In that setting, instead of working with a single sequent (a set of premises alongside a set of possible conclusions) we work with a list of sequents. In this paper,…
-
Discussing “Modal Logic”
I learned modal logic from a book by Hughes and Cresswell, a pair of philosophers from my home city of Wellington, so it was interesting for me to see the very different approach taken in this week’s book, which is now the standard reference for the field ( along with the Chargrov- Zakharyaschev book of…
-
Discussing “On Intuitionistic Diamonds (and Lack Thereof)”
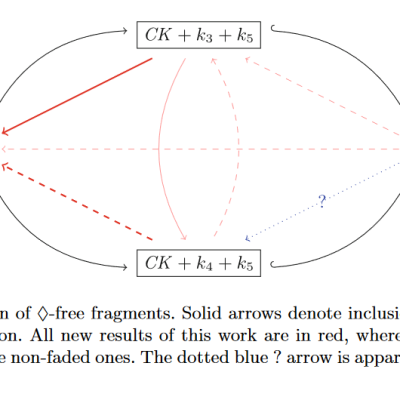
I choose papers for this blog by looking at the most cited papers in my Google Scholar recommendations of recent papers. This week, my algorithm has read my mind by recommending a fairly new paper that was already at the top of my list of papers to read. Its topic, as with a few papers…
-
Discussing “A modality for recursion”
The algorithm I use to choose reading for this blog, pulling the most cited papers out of my Google Scholar recommendations of new papers, sometimes pops out work close to my heart; quite a few years of my own research have been direct outshoots from this paper, following its adoption by Birkedal et al., and…
-
Discussing “On modal logic with an intuitionistic base”
There is a mini-theme on this blog of important developments in intuitionistic modal logic, in which the modal notion of necessity (and, less often, possibility) is blended with the intuitionistic notion of constructive proofs which denies, for example, the law of the excluded middle. We’ve read through Plotkin and Stirling, Simpson, Davies and Pfenning, and,…
-
Discussing “Associative n-Categories”
I have looked at PhD dissertations for this blog before, but never one this gargantuan; at 503 pages it weighs in at 3-4 times longer than the average thesis. The author does not quite apologise for the length, but at least acknowledges it, saying “[the] length of this thesis should by no means deter the…
-
Discussing “A Mechanization of the Blakers–Massey Connectivity Theorem in Homotopy Type Theory”
I first became aware of this paper from a long and fascinating blog comment thread in which mathematicians argued about the utility, or lack thereof, of homotopy type theory for homotopy theorists. Urs Schreiber, arguing for team HoTT, held up this paper an exemplar of the value of the type theoretical approach, saying “it was…
-
Discussing “Interactive Theorem Proving and Program Development. Coq’Art: The Calculus of Inductive Constructions”
I’ve written before about the Coq Proof Assistant . Since then, after years of bravely ignoring the sniggers its French name produced among English speakers, the developers have decided to remain it Rocq in honour of Rocquencourt, the French town in which much of the development took place. The good news for the authors of…
Categories
Recent Posts
- Discussing “A semantics for concurrent separation logic”
- Discussing “Z3: An Efficient SMT Solver”

- Discussing “BI as an Assertion Language for Mutable Data Structures”
- Discussing “Sheaves in Geometry and Logic”
Tags
1994 1996 2000 2001 2007 2014 2019 2021 2023 Abhishek Anand Andrew W. Appel Bedrock Systems Cambridge Tracts in Theoretical Computer Science Carnegie Mellon University Christopher D. Richards City University of New York Coq Cubical Type Theory Cyril Cohen Côte d'Azur University Inria Nantes INRIA Rocquencourt intuitionistic logic intuitionistic modal logic Journal of Automated Reasoning LICS Matthieu Sozeau Metaprogramming modal logic Notre Dame Journal of Formal Logic Paul-André Melliès POPL Princeton University Proof theory Rocq Saarland University Simon Boulier Théo Winterhalter types type theory University of Amsterdam University of Birmingham University of Cambridge University of Oxford Valeria de Paiva